Invited speakers
강경근 (연세대)
강명주 (서울대)
고동남 (카톨릭대)
김도현 (성신여대)
김정호 (경희대)
박진영 (한양대)
배기찬 (서울대)
배한택 (유니스트)
배형옥 (아주대)
변준혁 (서울대)
석진명 (서울대)
이동현 (포스텍)
이지훈 (중앙대)
이 호 (경희대)
장진우 (포스텍)
정진욱 (전북대)
조승연 (경상대)
채명주 (한경대)
최영필 (연세대)
하승열 (서울대)
홍영훈 (중앙대)
황병훈 (상명대)
Organizer
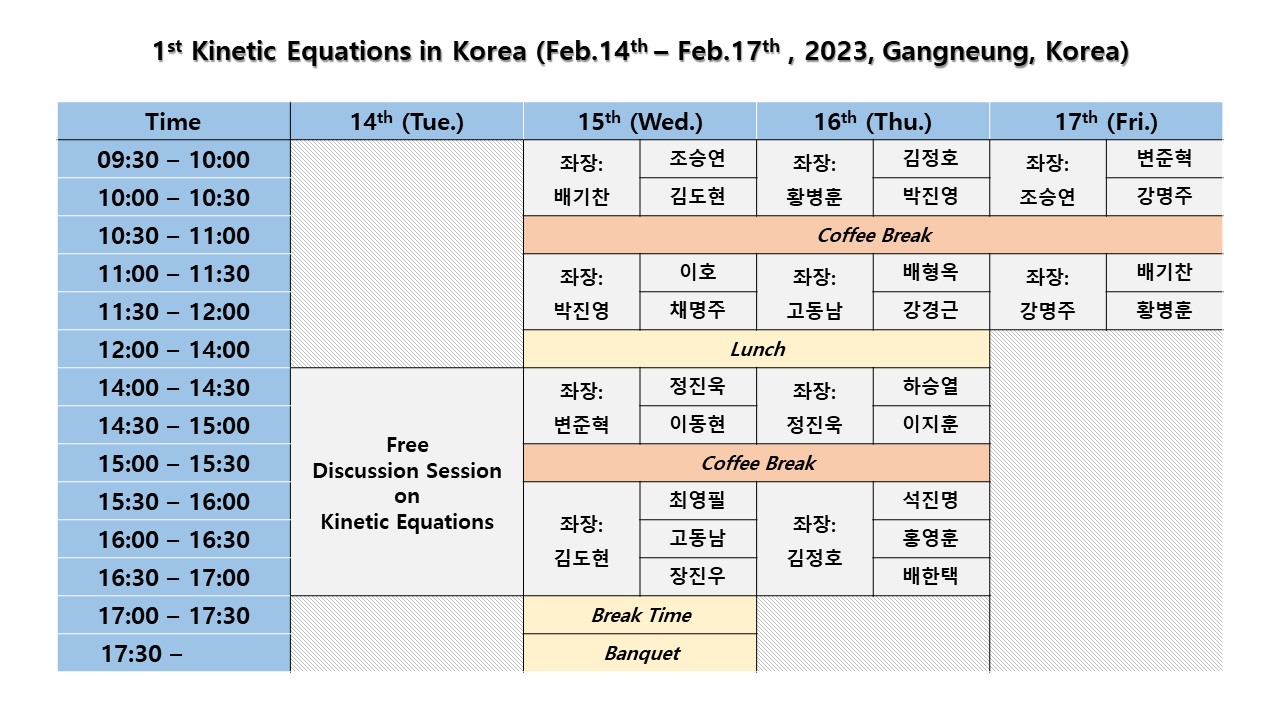
윤석배 (성균관대)Time table
Abstract
2023년 2월 15일
09:30 - 10:00
Seung-Yeon Cho (Department of Mathematics, GNU)
Title: A conservative semi-Lagrangian scheme for the rarefied gas dynamics
Abstract:
In this talk, we introduce a high order conservative semi-Lagrangian scheme for the Boltzmann equationn. In particular, we aim to construct an efficient scheme for the rarefied gas flow where the Knudsen number is large. We use semi-Lagrangain approach for treating convection term and the fast spectral method to compute the collision operator. In order to preserve conservative quantities, we adopt a conservative reconstruction and L 2 -minimization techniques. Contrary to existing numerical schemes, we do not use any time splitting approach, which enable us to obtain high accuracy. Numerical evidences will be provided to show that the proposed semi-Lagrangian method works better than its Eulerian counterpart in terms of stability and accuracy. This is the joint work with two UNICT professors, G. Russo and S. Boscarino.
10:00 - 10:30
Dohyun Kim (School of Mathematics, Statistics and Data Science, Sungshin Women’s University)
Title: Fokker-Planck-type aggregation equations on the sphere and the unitary group
Abstract:
In this talk, we introduce Fokker-Planck-type aggregation equations on the sphere and the unitary group that can be rigorously derived from stochastic particle systems through the meanfield limit. For both equations, we show that they admit global unique solutions and that incoherent states are stable when the diffusion effect is relatively small.
11:00 - 11:30
Ho Lee (Department of Mathematics, Kyung Hee University)
Title: Homogeneous solutions of the Einstein-Boltzmann system for massless particles
Abstract:
In this talk we study the Cauchy problem for the Einstein-Boltzmann system in a spacetime having an isotropic singularity. Initial data will be given at the initial singularity in a suitable sense, and the particles will be assumed to be massless near the initial singularity. We obtain the local existence of spatially homogeneous solutions for certain range of soft potentials.
11:30 - 12:00
Myeongju Chae (School of computer engineering and applied mathematics, HKNU)
Title: Nonlinear instability of rolls in the 2–dimensional generalized Swift–Hohenberg equation
Abstract:
We discuss on a nonlinear instability for localized perturbation of roll waves bifurcating from an equilibrium in the 2–dimensional generalized Swift–Hohenberg equation.
14:00 - 14:30
Jinwook Jung (Department of Mathematics, Jeonbuk National University)
Title: Strong solutions to the kinetic equations coupled with compressible viscous fluid equations
Abstract:
In this talk, we discuss the existence and uniqueness of strong solutions to the kinetic equations coupled with compressible Navier-Stokes equations. Here the coupling of two equations is through a friction (or drag) force which depends on the density of the compressible fluid and the relative velocity between particles and fluid. Presenting two examples, i.e. Vlasov-NavierStokes model and BGK-Navier-Stokes model, we stress that for the existence in L 2 -Sobolev spaces, exponential weight on the kinetic density in the velocity variable is crucial due to the fluid density in the coupling term. Then we show that when such an exponential weight is imposed on the kinetic density, we can find a unique strong solution locally in time. This talk is based on the joint work with Y.-P. Choi (Yonsei University).
14:30 - 15:00
Donghyun Lee (Department of Mathematics, POSTECH)
Title: H¨older regularity of the Boltzmann equation past an obstacle
Abstract:
Regularity and singularity of the solution according to the shape of domains is a challenging research theme in the Boltzmann theory. In this talk, we study optimal C 1/2− regularity of the hard-sphere Boltzmann equation exterior of an uniformly convex obstacle with specular reflection boundary condition. This is joint work with Chanwoo Kim.
15:30 - 16:00
Young-Pil Choi (Department of Mathematics, Yonsei University)
Title: Global existence of weak solutions for nonlinear Vlasov–Poisson–Fokker–Planck equations
Abstract:
We consider the Vlasov–Poisson system with the nonlinear Fokker–Planck term which depends on the associated hydrodynamic fields of mean velocity and temperature. For the nonlinear Vlasov–Poisson–Fokker–Planck, we establish the global-in-time existence of weak solutions.
16:00 - 16:30
Dongnam Ko (Department of Mathematics, Catholic University of Korea)
Title: On the stochastic synchronization of the Winfree model with a multiplicative noise
Abstract:
We study stochastic almost-sure convergence of the stochastic collective behavior models with multiplicative noise. As an example, we consider the Winfree model. It is well-known that the additive white noise affects the dynamics as with the heat kernel, which makes the solution profile spread into the phase domain. In contrast, the multiplicative noise can be understood that the communication weight in the interaction network get affected by Brownian motion. The geometric Brownian motion is such a case, which shows exponential convergence to an equilibrium. In this talk, we establish stochastic convergence to an equilibrium of a general gradient system when the noise strength is small enough. This talk is based on a joint work with Seung-Yeal Ha (SNU) and Woojoo Shim (KIAS).
16:30 - 17:00
Jin Woo Jang (Department of Mathematics, POSTECH)
Title: Kinetic Models for Semiflexible Polymers in a Half-plane
Abstract:
In this talk, we introduce a derivation of a kinetic equation for semi-flexible polymers. The equation describes the limiting behavior of a N-segment discrete chain via the continuum-limit. In the half-plane, we also present a formal derivation of the trapping boundary condition by assuming the energy-minimizing transition of a segment at the boundary. Then we will briefly introduce the proof of global well-posedness, long-time asymptotic behavior, hypoellipticity, and the H¨older regularity of solutions near the boundary.
2023년 2월 16일
09:30 - 10:00
Jeongho Kim (Department of Applied Mathematics, Kyung Hee University)
Title: Asymptotic analysis of a Vlasov-Fokker-Planck/magnetohydrodynamic system
Abstract:
We study an asymptotic analysis of the coupled system of the Vlasov-Fokker-Planck (VFP) equation and magnetohydrodynamic (MHD) equations, where two systems are coupled via drag force. In particular, we consider the case when the velocity of the particle is also relaxed to the locally averaged velocity. We consider the regime where the local-alignment and diffusion force are strong, so that the solution to the VFP/MHD system converges to the Euler/MHD system, as the singular parameter tends to zero. To attain a rigorous convergence analysis, we rely on the celebrated relative entropy method.
10:00 - 10:30
Jinyeong Park (Department of Mathematics, Hanyang University)
Title: Emergent dynamics of the swarmalator model and its mean-field limit
Abstract:
We introduce the swarmalator model which describes the dynamics of interactive particles that simulatneously swarm and sync. In this model, we employ the singular attractive-repulsive coupling for the particle aggregation, while we use the Kuramoto-type interaction for the phase synchronization. In this talk, we survey the emergent behavoirs of the particle system and induce the mean-field limit of the swarmalator model.
11:00 - 11:30
Hyeong-Ohk Bae (Department of Financial engineering, Ajou University)
Title: Online Optimization by Consensus Based Optimization Algorithm with Average Drift
Abstract:
Tracing a moving objective in a changing high dimensional space is a prevalent but difficult optimization problem. We propose an applied consensus-based optimization algorithm with average drift for tracking a moving optima. We show the convergence to the global minimizer of the applied CBO and verify the algorithm’s performance in approximating static and dynamic objective function. In numerical simulations, we apply the suggested CBO algorithm to online portfolio selection (OPS) in finance. Our CBO improves the speed of searching while lowering tracking errors than the CBO with adaptive momentum (Adam-CBO). We prove the regret bound of the ADAD-CBO.
11:30 - 12:00
Kyungkeun Kang (Department of Mathematics, Yonsei University)
Title: Kinetic models of Keller-Segel equations and Vlasov equation with a flocking term coupled to incompressible fluid flow
Abstract:
Topics that are discussed in this talk are two-fold. Firstly, a kinetic model related to the Keller-Segel model is concerned, and we show that such model is globally well-posed. The existence of a macroscopic diffusion limit of the kinetic model is also proved. Secondly, we study Vlasov-fluid equaitons with a flocking term such as Vlasov-Navier-Stokes equation in 2D and Vlasov-Stokes system in 3D. Temporal decay and asymptotic behaviors of solutions are analysed.
14:00 - 14:30
Seung Yeal Ha (Department of Mathematical Sciences, Seoul National University)
Title: Finiteness of collisions and phase-locking for the Kuramoto model
Abstract:
We discuss relations between the finiteness of collisions and phase-locking of the Kuramoto model. When there is no inertial effect, it is well known that the finiteness of collisions is equivalent to the emergence of phase-locking. Thus, when a Kuramoto ensemble is under the effect of inertia, whether the same equivalence relation hold or not is an intricate question. In this talk, we show that in a small inertia regime, the aforementioned equivalence still holds, whereas in a large inertia regime, we show that a homogeneous Kuramoto ensemble with the same natural frequencies can exhibit phase-locking, while there are countable number of collisions between Kuramoto oscillators. This is a contrasted effect of a large inertia in phase-locking process. This is a joint work with Hangjun Cho (SNU) and Jiu-Gang Dong (Dalian Univ. of Technology).
14:30 - 15:00
Jihoon Lee (Department of Mathematics, Chung-Ang University)
Title: On the Chemotaxis-Navier-Stokes Equations
Abstract:
We consider the construction of the weak solutions to the chemotaxis-Navier-Stokes equations. Also we consider the temporal decay of the solutions to the chemotaxis-Navier-Stokes equations. This is the joint work with Kyungkeun Kang and Michael Winkler.
15:30 - 16:00
Jinmyoung Seok (Department of Mathematics Education, SNU)
Title: Quantum-Classical Correspondence of White Dwarfs
Abstract:
In 1930, a mathematical description of white dwarfs was suggested by a theoretical physicist S. Chandrasekhar who also calculated the limit mass of white dwarfs. In his theory, a white dwarf is given by a steady solution of the classical hydrostatic equation with a specific equation of state derived from the special relativistic kinetic energy formula. Nowadays, the white dwarfs are also described by the quantum ground states of the relativistic Hartree-Fock equation, which is a mean-field equation of the multi-body Schr¨odinger equation. In this talk, we are interested in the consistency of these two quantum and classical theories for white dwarfs. We will see that this might be done by introducing, as a middle step, a kinetic formulation of white dwarfs, which is given by the fermionic ground states for the relativistic Vlasov-Poisson equation.
16:00 - 16:30
Younghun Hong (Department of Mathematics, Chung-Ang University)
Title: Lieb-Thirring inequalities and Strichartz estimates for orthogonal functions
Abstract:
This is a survey talk. We discuss Lieb-Thirring inequalities and Strichartz estimates for orthogonal functions. These inequalities extend well-known Gagliardo-Nirenberg inequalities and Strichartz estimates for single wave functions, but they improve summability exploiting orthogonality. The inequalities have numerous applications in math physics, for instance, in proving stability of matter. Among many others, we will be focused on their roles in semiclassical analysis and their connection to the analogous inequalities for kinetic distribution functions.
16:30 - 17:00
Hantaek Bae (Department of Mathematical Sciences, UNIST)
Title: Well-posedness of Viscous Water-Waves
Abstract:
In this talk, we discuss a nonlinear model of the viscous water-waves system proposed by Dias-Dychenko-Zakharov (DDZ). We first study the linear model of DDZ. We then derive a new approximated model of DDZ and show how to find a global-in time solution.
2023년 2월 17일
09:30 - 10:00
Junhyeok Byeon (Department of Mathematical Sciences, Seoul National University)
Title: Asymptotic dynamics for the Cucker–Smale-type model with the velocity control
Abstract:
We study the collective behaviors of the second-order nonlinear consensus model with velocity control. The proposed model includes the speed-regulated, relativistic, and almost unit-speed models. By the subsystem analysis, we provide conditions for the mono or bi-cluster flocking and study the regularity of a solution under a singular kernel.
10:00 - 10:30
Myeongju Kang (Institution)
Title: Continuum limit of Lohe model on some class of Lie groups
Abstract:
The Lohe model is a generalized high dimensional Kuramoto-type model whose oscillators lie on a special class of matrix Lie group. The continuum Lohe model is a time-evolutionary integro-differential equation which governs the Lohe phase field, and solution to the Lohe model becomes a simple function valued solution to the continuum Lohe model. In this talk, we study the emergent dynamics and global well-posedness of the continuum Lohe model which can be obtained by a continuum limit of the Lohe model. We first construct a local solution to the continuum Lohe model. Then, we find an invariant set to extend our local solution to a global one. Lastly, we show that sequence of simple functions obtained from the Lohe model converges to a solution of the continuum Lohe model in supreme norm sense. This talk is based on the joint work with Hangjun Cho and Seung-Yeal Ha.
11:00 - 11:30
Gi-Chan Bae (Research institute of Mathematics, SNU)
Title: Large amplitude solution of BGK model
Abstract:
Bhatnagar–Gross–Krook (BGK) equation is a relaxation model of the Boltzmann equation which is widely used in place of the Boltzmann equation for the simulation of various kinetic flow problems. In this work, we study the asymptotic stability of the BGK model when the initial data is not necessarily close to global equilibrium pointwisely. The main difficulty of the BGK equation comes from the highly nonlinear structure of the relaxation operator. To overcomes this issue, we derive refined control of macroscopic fields to guarantee the system enters a quadratic nonlinear regime, in which the highly nonlinear perturbative term relaxes to essentially quadratic nonlinearity after a long but finite time. This is joint work with G.-H. Ko, D.-H. Lee and S.-B. Yun.
11:30 - 12:00
Byung-Hoon Hwang (Department of Mathematics Education, SMU)
Title: Global existence of weak solutions to a BGK model relaxing to the barotropic Euler equations
Abstract:
A kinetic BGK model leading to the barotropic Euler equations in the hydrodynamic limit was introduced by Bouchut [J. Stat. Phys., 95, (1999), 113–170]. In the mono-dimensional case, the global-in-time existence of weak solutions and its hydrodynamic limit were studied, but the multi-dimensional case has not been established yet. In this talk, we discuss the globalin-time existence of weak solutions to the BGK-type model proposed by Bouchut. Note that our existence theory makes the hydrodynamic limit from the BGK-type equations to the multidimensional barotropic Euler system discussed by Berthelin and Vasseur [SIAM J. Math. Anal., 36, (2005), 1807–1835] completely rigorous.

